 Home
Articles
Notes
Projects
Home
Articles
Notes
Projects
Advent of code - if you're unaware - is an yearly event where you are given a programming puzzle to solve daily from December 1st to 25th. This was my 3rd year participating, and now that the dust has settled, I'd like to document some of the new and interesting things I've learned this year. If you want to take a look at the actual code, all my solution can be found in this repo.
This should go without saying but: this article WILL contain spoilers. So if you haven't yet done this year's puzzles and want to avoid spoilers, you have been warned. I'll try to give a small refresher on the puzzles when talking about them, but since I don't want to repeat everything here, I'll assume that you're somewhat familiar with the puzzles. If not, you can find each day's puzzle at the adventofcode website, for example day 1 link would be https://adventofcode.com/2023/day/1.
I usually try to pick up a new language each year. Something that's different than what I tend to use in order to not get stuck in a rut. But since the last couple months were quite hectic for me, I decided to go with something that I already had a bit of familiarity with rather than picking up something completely new.
If I had to summarize my view on Lua in one sentence, "I can work with it, but it's not a joyful experience." As far as dynamic languages go at least, it doesn't have a singular fatal flaw which disqualifies it for me. It's small, fast and fairly cohesive thanks to it's "everything is a table" philosophy.
But there's just way too many small annoyances that build up and ruin the mood.
The lack of many many really basic functionalities is very apparent - no
builtin way to retrieve the number of items in a table despite tables being the
central theme of the language, no compound operators (e.g +=), no continue
resulting in unnecessary deep nesting - the list the just goes on.
Misfeatures like inclusive 1 based indexing don't help either.
As said, none of this is fatal, I can easily work around these issues - but it leaves a bitter taste. But instead of endlessly complaining about this, let's just move on to the fun stuff: the interesting lessons that I've learnt.
Day 10 was the first puzzle this year that I would consider hard. In short, you are given the integer 2d co-ordinates of a loop and are asked to figure out how many points are interior to the loop.
Initially I tried to solve this by ray casting, but unfortunately I was messing up the cases where the ray and the border are going in the same direction. After sleeping on it, I decided to take a different approach, "If I can figure out the area of the loop, that should be my answer." It turned out that this wasn't correct, but gave me a direction to follow at the time.
Looking up Wikipedia for calculating area of polygon lead to the shoelace
formula and the following video give some visual intuition on
how it worked.
But after implementing it, I noticed that the resulting area was higher than the
answer for the example input.
Thinking that it's due to the area including the borders, I decided to subtract
the number of borders, but that resulted in an answer too low.
After a bit more playing around I realized that area - (borders / 2) + 1 works
and gives the expected answer, though at that time I didn't know why.
Curious, I looked for answers and came to realize that the above formula is effectively just pick's theorem. And the reason why the area wasn't equal to the interior points is because the area calculation neither fully includes the border nor fully excludes them.
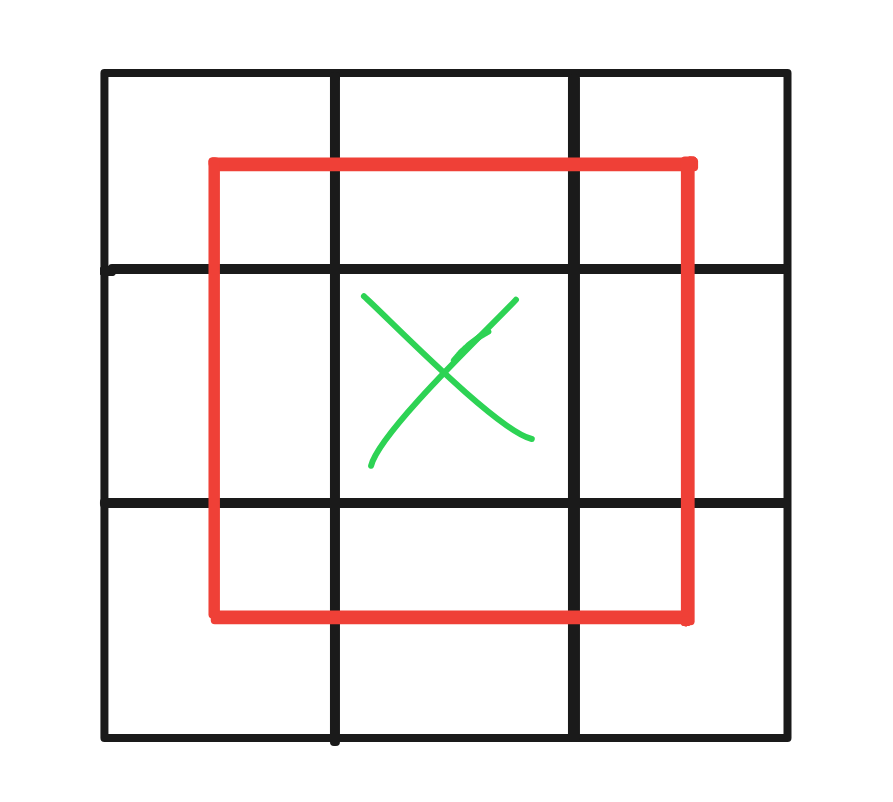
Instead of you have something like above example - a 3x3 grid where the borders
are all except the interior middle point (marked green) and the area is marked
by the smaller red rectangle.
The top, bottom, left, right borders are half-included, which explains the
borders/2.
And the corner borders are quarter-included which explains the +1,
well... at least for a simple rectangle that is.
I'm not fully sure why the +1 works even in case of arbitrary simple polygon,
but my curiosity ran out at that point.
Regardless, there was something about the shoelace formula that appeared quite elegant to me, and so it stuck around in the back of my head. This ended up being pretty helpful at day 18 where I immediately recognized that the problem can be solved with shoelace + pick again since it was a very similar puzzle to day 10.
The problem is essentially telling you to implement a chained hash-table. There are 256 slots where you need to insert, update and remove entries from. The catch here is that you need to maintain the insertion order within each slot in order to calculate the final result.
Since the actual input isn't too large, you can simply get away with using 256 dynamic arrays as each slot. However if you want to optimize of efficiency, especially at large N, then this isn't a good idea since:
Using a linked list instead of dynamic arrays allows for O(1) removal. And if you keep track of the "tail" pointer, then you also have O(1) append similar to a dynamic array. But you'd still need to linear search through the list in order to find the element, though.
This is where an intrusive list comes into play.
Intrusive list - in case you're unaware - is when you embed the next and/or
prev pointers directly into your data rather than it being in some external
"container".
This allows us to simply use 256 different hash-tables as our slots where the
insertion order is maintained via the embedded list pointers.
With this, we get best of both worlds, O(1) lookups along with O(1) removal and
insertion.
This is quite frankly a pretty good solution. However I went with a slightly simpler and a bit unorthodox method instead. One key observation here was that the insertion order only matters when calculating the score at the end. This means that we're free to keep things unordered as long as we can recover the insertion order later on.
And so instead of embedding a next pointer into the data and maintaining a linked list, what I did was embed an "epoch counter" instead. An "epoch counter" here basically means an integer that gets incremented each time a new node is inserted.
local epoch = 0 -- initially zero
-- when inserting a item into a slot, also add the epoch
table.insert(slot[N], { item, epoch })
epoch = epoch + 1 -- increment the epoch counter
This effectively gives us a "time-stamp" at which a certain node was inserted. So at the end - where the order matters - we simply sort each slot by this time-stamp to recover the insertion order.
Assuming your language of choice has a sorting routine readily available (a safe assumption), this makes things much easier to implement. In fact, following this strategy, you could get away with just a single hash-table instead of having 256 of them for each slot. Simply embed the slot number into the node as well and then sort by the slot first, and epoch second to recover the ordering.
Day 17 (the way I solved it at least) required a priority queue. Heaps are the usual choice when implementing priority queue - so much so that these two terms are often used interchangeably. While I do have some prior experience in partially implementing heap, I hadn't yet needed to implement it fully, and so this was a good opportunity to learn. You can go about implementing heaps in two ways:
i * 2 for the left child
and i * 2 + 1 for the right child.I decided to go the implicit route because I assumed it'd be easier to work with arrays in lua than trees. Pushing was fairly simple, though implementing popping turned out to be more involved than I had imagined. But after you do it once things "click in" and it becomes much easier to do it again.
As a follow up I decided to implement a generic min-heap in C.
The key feature here is that the heap implementation doesn't assume anything
about how to allocate memory, which gives the user choice to pick whichever
method is appropriate for their situation: a typical dynamic array backed by
malloc/realloc, or perhaps backed by a custom allocator, or when
the upper bound is known to be small even just a fixed size array allocated on
the call-stack would work fine.
Day 24 part 1 gives you a couple starting co-ordinates along with velocity and asks you to find the intersection point. I could guess that this was some sort of linear algebra problem, but linear algebra doesn't really come up on my day to day task so I haven't bothered learning it.
Although my math was lacking, some problem solving skill came in clutch.
Assuming that the intersection does happen, at that point the x and y
co-ordinates of both lines must be equal.
Which basically gives us the following equation where A and B are the starting
co-ordinates, Av and Bv are the velocity of A and B respectively, and
At and Bt are the time of the intersection (which need not be the same since
we're only looking for path intersection, not collision):
A + Av * At == B + Bv * Bt
At := (B + Bv * Bt - A) / Av
Bt := (A + Av * At - B) / Bv
This by itself wasn't very helpful.
In order to solve At we need to know the value of Bt, and in order to solve
Bt we need to know the value of At.
The trick here was to simply assume a value for one and calculate the
value for the other.
Let's say we assume At is 5 and with that assumption calculate Bt to be 10.
Now we can plug these values into our initial equation and check if both sides
are equal or not.
If they are, then our guess was right and we got the answer.
If they aren't, then take a new guess based on whether we were overshooting or
undershooting and repeat.
This algorithm is also known as Newton-Raphson method.
However, a couple subtleties come into play. First of all, you'd need to bound the loop iteration to some number because the lines may never intersect in case they're running in parallel. Secondly, the numbers in the actual input file is quite large which gives pretty bad floating-point rounding error. So when comparing for equality you need to allow for some leeway (this is true in general, but gets more important at larger numbers). For my input, an error margin of 0.02 works fine. Anything less produces incorrect results.
After I was done with the Newton-Raphson solution, I decided this would be a good opportunity to learn some linear algebra basics. 3Blue1Brown's Essence of Linear Algebra series on youtube turned out to be an immensely helpful resource for this. And with my newfound knowledge I decided to solve it again but this time using Cramer's rule. Nothing mind blowing if you're already familiar with linear algebra, but learning something new and applying it in practice (even if just to solve silly puzzles) is always an interesting experience.
Assuming you don't just import solution in python, this was bit of a difficult
puzzle considering it's the last day.
The puzzle is effectively asking you to find the global minimum cut of
an undirected, unweighted graph.
Though it's much easier than that since you are told that the minimum cut is 3,
you just need to find the number of nodes in each side of the cut.
Initially I just solved it by rendering the graph with graphviz and manually plucking out the cut, but the problem seemed interesting and at that point I wasn't yet aware of minimum cut or any of the algorithms associated with it, which meant it was another opportunity to learn something new.
After looking through wikipedia, it appears that most of the algorithms in this area are overly complicated for the puzzle - they are designed for directed weighted graph where each node also has a certain "capacity". So instead I solved it with a more ad-hoc approach loosely based on Stoer-Wagner.
The key observation here is that cutting a graph into two means that we will end up with two completely disconnected graphs. This is obvious and not very helpful, but if we reformulate the same thing in a different manner: if we pluck out a "sub-graph" and then disconnect it from the rest of the graph, then the "cut" of this sub-graph is equal to the edges going out of it. In other words, we need to find the sub-graph that has only 3 edges going out of it.
How do we make this "sub-graph"? By contracting edges. In simple terms, it means taking two nodes and mushing them into one. It's not too difficult to visualize how this might work, but how to do this in code? Wikipedia article on edge-contraction wasn't too helpful. But perhaps that's for the better since working it out on my own wasn't too difficult and actually pretty fun.
local supernode = {
nodes = {} -- a set of nodes that was "consumed" into the sub-graph
edges = {} -- a map of edges that are going out from the sub-graph
}
That lays the groundwork. Initially the sub-graph starts empty so it contains no edges and no nodes. Then we simply start consuming nodes one after another until we find the cut of 3. Consuming a node involves 3 main steps (doesn't have to be performed in order):
The last step is a bit tricky, when inheriting edges, we need to actually keep track of how many edges the sub-graph has to a certain outside node. For example, if we had a graph like the following:
A <-> C
B <-> C
And we wanted to disconnect A and B from C then we'd have to cut two
edges, not one.
Which is why unlike the nodes member, edges member is a map of how many
edges to a certain node we have instead of being a set.
Putting this all down in pseudo code:
supernode.nodes[node_to_consume] = true -- consume the node
supernode.edges[node_to_consume] = nil -- remove edges to this node
for edge in get_edges(node_to_consume) do
-- skip edges pointing into the sub-graph itself
if (supernode.nodes[edge]) then continue end
-- increment the number of edges by one
-- (assume initailized to 0 if previously non-existant)
supernode.edges[edge] += 1
end
Now we just repeat the process, consuming the most "tightly connected" node (i.e the node that has most number of edges into our sub-graph), until we've found the sub-graph with the cut of 3.
In majority of the cases, this will find the cut in the first iteration. But unlike Stoer-Wagner, which does an exhaustive V-1 iteration, my algorithm is not deterministic. And so you'd need to run it a bunch of times with different starting points. Although majority of the times (~9/10) it will find the cut in the first iteration. Not ideal, but good enough to solve the puzzle and good enough for me!
Here are two solutions which aren't mine, but I've found them interesting enough to list out:
Though I didn't find this year as fun as last year, it was nevertheless a good learning opportunity and still pretty fun. Looking forward to next year, until then!